Binary Fuse Filters: Fast and Tiny Immutable Filters

Daniel Lemire
professor, Data Science Research Center
Université du Québec (TÉLUQ)
Montreal

blog: https://lemire.me
twitter: @lemire
GitHub: https://github.com/lemire/

Probabilistic filters?

• Is in the set ?
• Maybe or definitively not

Usage scenario?

• We have this expensive database. Querying it cost you.
• Most queries should not end up in the data.
• We want a small 'filter' that can prune out queries.

Theoretical bound

• Given elements in the set
• Spend bits per element
• Get a false positive rate of

Usual constraints

• Fixed initial capacity
• Difficult to update safely without access to the set
• To get a 1% false-positive rate: bits?

Hash function

• From any objet in the universe to a word (e.g., 64-bit word)
• Result looks random

uint64_t murmur64(uint64_t h) {
  h ^= h >> 33;
  h *= UINT64_C(0xff51afd7ed558ccd);
  h ^= h >> 33;
  h *= UINT64_C(0xc4ceb9fe1a85ec53);
  h ^= h >> 33;
  return h;
}

Conventional Bloom filter

• Start with a bitset .
• Using k hash functions .

Adding an element

• Given an object from the set, set up to k bits to 1

Checking an element

• Given an object from the universe, set up to k bits to 1

Checking an element: implementation

• Typical implementation is branchy
• If not , return false
• If not , return false
• ...
• return true

  uint64_t hash = hasher(key);
  uint64_t a = (hash >> 32) | (hash << 32);
  uint64_t b = hash;
  for (int i = 0; i < k; i++) {
    if ((data[reduce(a, length)] & getBit(a)) == 0) {
      return NotFound;
    }
    a += b;
  }
  return Found;

False positive rate

Bloom filters: upsides

• Fast construction
• Flexible: excess capacity translates into lower false positive rate
• Degrades smoothly to a useless but 'correct' filter

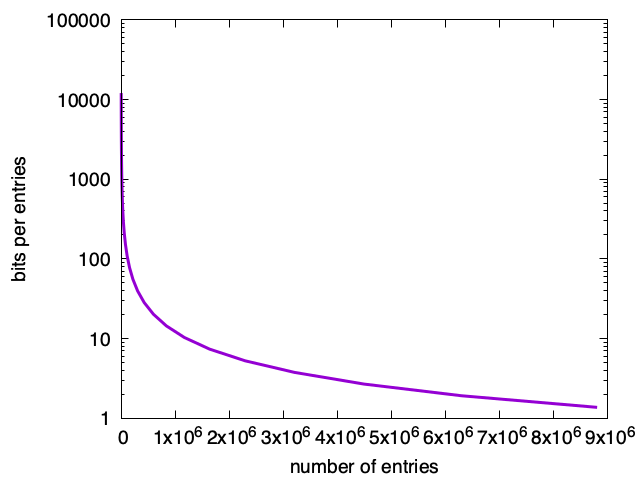
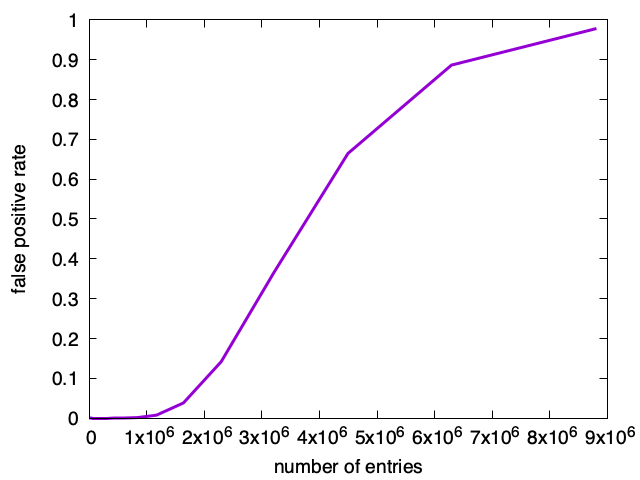
Bloom filters: downsides

• 44% above the theoretical minimum in storage
• Slower than alternatives (lots of memory accesses)

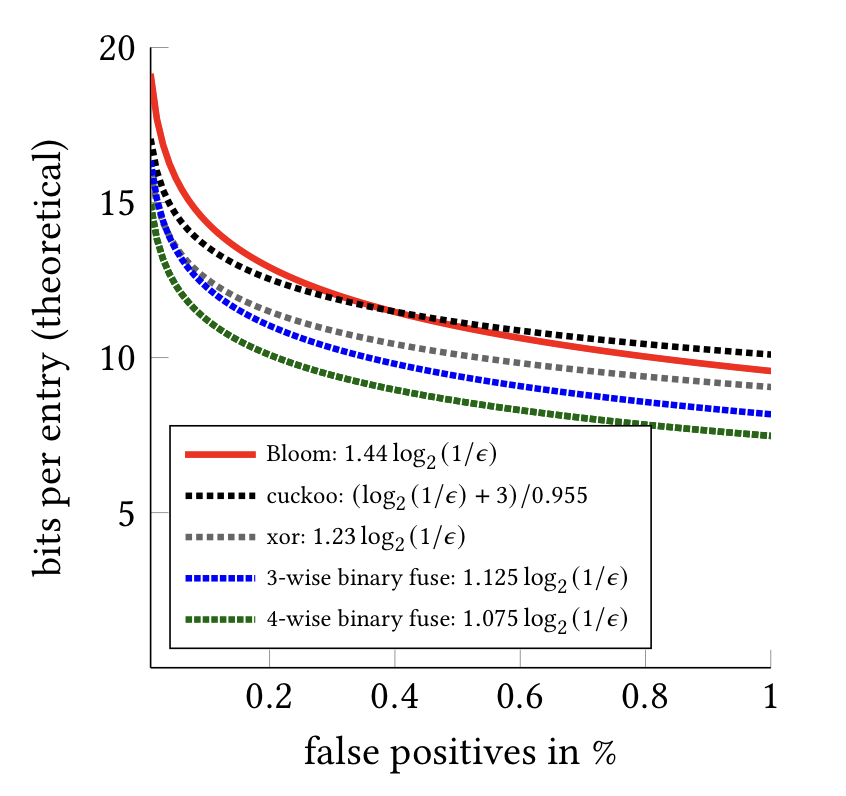
Memory accesses

(Intel Ice Lake processor, out-of-cache filter)

Mispredicted branches

(Intel Ice Lake processor, out-of-cache filter)

Performance

(Intel Ice Lake processor, out-of-cache filter)

Blocked Bloom filters

• Same as a Bloom filters, but for a given object, put all bits in one cache line
• Optional: Use SIMD instructions to reduce instruction count

Blocked Bloom filters: pros/cons

• Stupidly fast in both construction and queries
• ~56% above the theoretical minimum in storage

  auto hash = hasher_(key);
  uint32_t bucket_idx = reduce(rotl64(hash, 32), bucketCount);
  __m256i mask = MakeMask(hash);
  __m256i bucket = directory[bucket_idx];
  return _mm256_testc_si256(bucket, mask);

Binary fuse filters

• Based on theoretical work by Dietzfelbinger and Walzer
• Immutable datastructure: build it once
• Fill it to capacity
• Fast construction
• Fast and simple queries

Arity : 3-wise, 4-wise

• 3-wise version has three hits, 12% overhead
• 4-wise version has four hits, 8% overhead

Queries are silly

• Have an array of fingerprints (e.g., 8-bit words)
• Compute 3 (or 4) hash functions:
• Compute fingerprint function ( 8-bit word)
• Compute XOR and compare with fingerprint:
  

bool contain(uint64_t key, const binary_fuse_t *filter) {
  uint64_t hash = mix_split(key, filter->Seed);
  uint8_t f = fingerprint(hash);
  binary_hashes_t hashes = hash_batch(hash, filter);
  f ^= filter->Fingerprints[hashes.h0] ^ filter->Fingerprints[hashes.h1] ^
       filter->Fingerprints[hashes.h2];
  return f == 0;
}

(Intel Ice Lake processor, out-of-cache filter)

(Intel Ice Lake processor, out-of-cache filter)

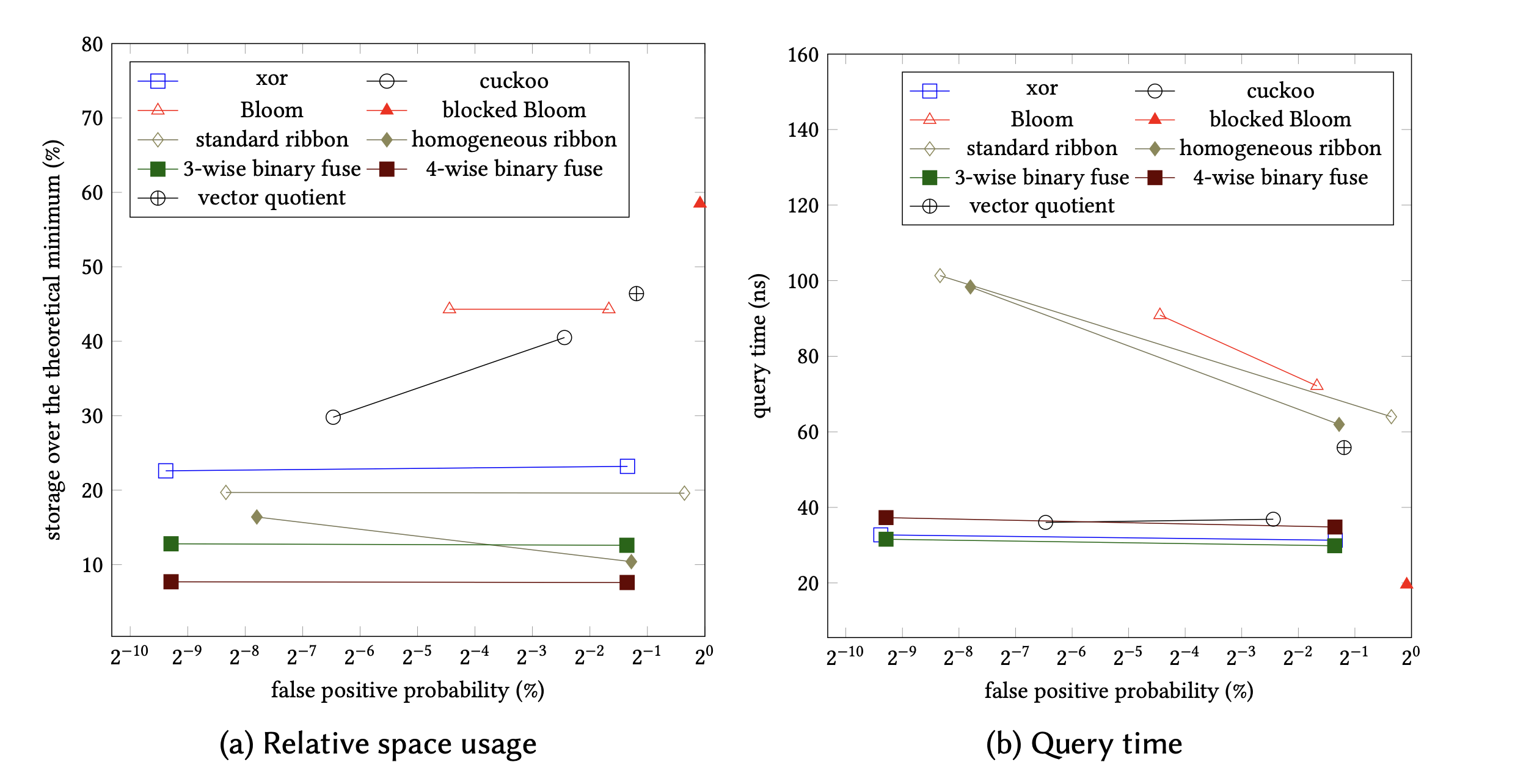
Construction 1

• Start with array for fingerprints containing slightly more fingerprints than you have elements in the set
• Divide the array into segments (e.g., 300 disjoint)
• Number of fingerprints in segment: power of two (hence binary)

Construction 2

• Map each object in set, to locations , ,
• The locations should be in three consecutive segments (so relatively nearby in memory).

Construction 3

• At the end, each location is associated with some number of objects from the set

Construction 4

• Find a location mapped from a single set element , e.g.,
• Record this location which is owned by
• Remove the mapping of to locations , ,
• Repeat

Construction 5

• Almost always, the construction terminates after one trial
• Go through the matched keys, in reverse order, adn set (e.,g.)

Construction: Performance

• Implemented naively: terrible performance (random access!!!)
• Before the construction begins, sort the elements of the sets according to the segments they are mapped to.
• This greatly accelerates the construction

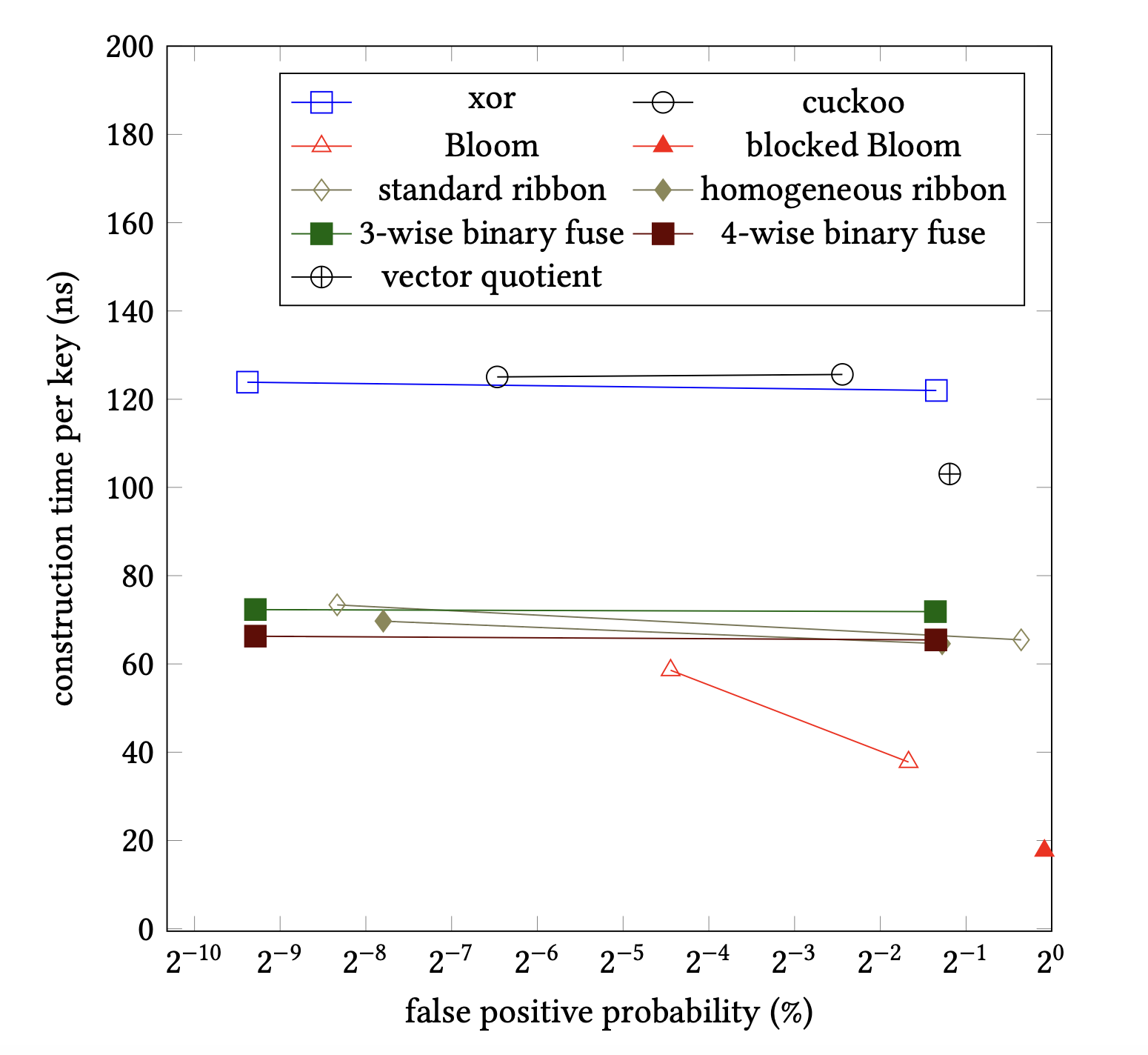
How does the performance scale with size?

For warm small filters, number of access is less important.
Becomes more computational.

For large cold filters, accesses are costly.

10M entries

(Apple M2)

100M entries

(Apple M2)

Compressibility (zstd)

Sending compressed filters

Compressed (zstd) binary fuse filters can be within 5% of the theoretical minimum.

Some links

• Bloom filters in Go: https://github.com/bits-and-blooms/bloom
• Binary fuse filters in Go: https://github.com/FastFilter/xorfilter
• Binary fuse filters in C: https://github.com/FastFilter/xor_singleheader
• Binary fuse filters in Java: https://github.com/FastFilter/fastfilter_java
• Giant benchmarking platform: https://github.com/FastFilter/fastfilter_cpp

Other Links

• Blog https://lemire.me/blog/
• Twitter: @lemire
• GitHub: https://github.com/lemire