Accurate and efficient software microbenchmarks

Daniel Lemire
professor, Data Science Research Center
Université du Québec (TÉLUQ)
Montreal

blog: https://lemire.me
twitter: @lemire
GitHub: https://github.com/lemire/

Background

• Fastest JSON parser in the world (on commodity processors): https://github.com/simdjson/simdjson
• First to parse JSON files at gigabytes per second

Where is the code ?

All code for this talk is online (reproducible!!!)

https://github.com/lemire/talks/tree/master/2023/performance/code

How fast is your disk?

PCIe 4 drives: 5 GB/s reading speed (sequential)

PCIe 5 drives: 10 GB/s reading speed (sequential)

CPU Frequencies are stagnating

Fact

Single-core processes are often CPU bound

Solution?

Optimize the software.

Incremental optimization, how do you know that you are on the right track?

Hypothesis

This software change (commit) improves our performance.

Simple

Measure time elapsed before, time elapsed after.

Complex system

Software systems are complex systems: changes can have unexpected consequences.

JIT

Virtual Machine Warmup Blows Hot and Cold

System calls

System calls (especially IO) may dominate, assume that they remain constant. Idem with multicore and multi-system processes.

Data access

data structure layout changes can trigger expensive loads, assume that we keep that constant.

Tiny functions

Uncertainty principle: by measuring you are affecting the execution so that you cannot measure safely tiny functions.

Take statically compiled code

Transcoding UTF-16 to UTF-8 of an 80kB Arabic string using the simdutf library (NEON kernel).

Use the average?

Let be the true value and let be the noise distribution (variance ).

We seek .

Repeated measures increase accuracy

Measures are

Sum is . Variance is .

Average is . Variance is . Standard deviation of .

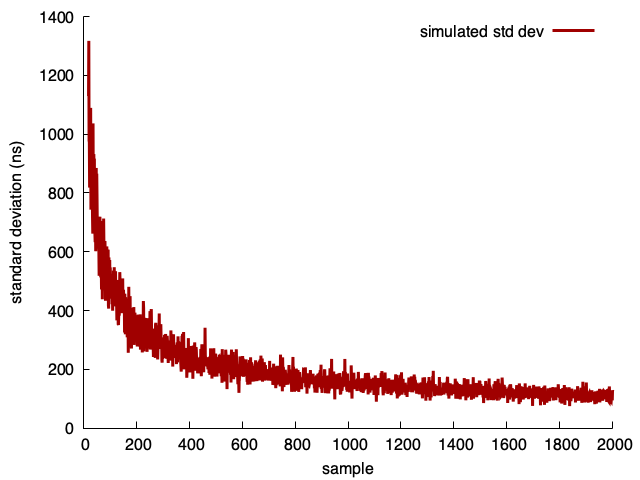
Simulation

mu, sigma = 10000, 5000
for N in range(20, 2000+1):
    s = [sum(np.random.default_rng().normal(mu, sigma, N))/N for i in range(30)]
    print(N,np.std(s))

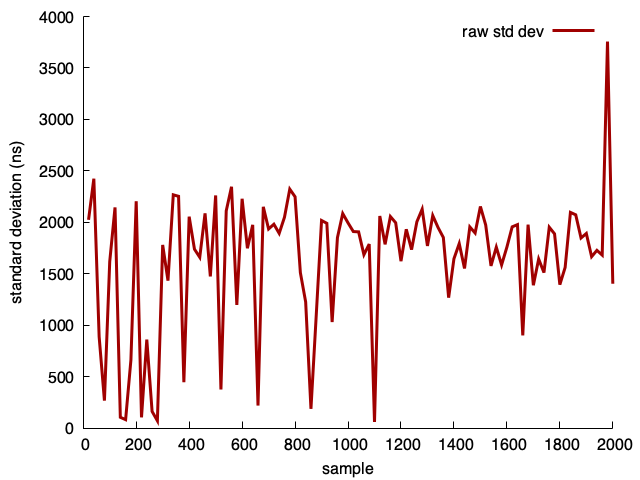
Actual measurements

// returns the average
double transcode(const std::string& source, size_t iterations);


...

  for(size_t i = iterations_start; i <= iterations_end; i+=step) {
    std::vector<double> averages;
    for(size_t j = 0; j < 30; j++) { averages.push_back(transcode(source, i)); }
    std::cout << i << "\t" << compute_std_dev(averages) << std::endl;
  }

Sigma events

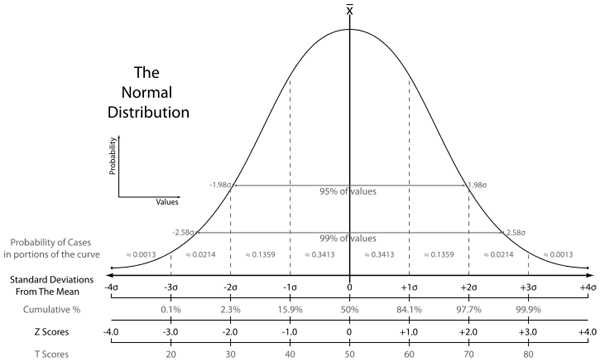
• 1-sigma is 32%
• 2-sigma is 5%
• 3-sigma is 0.3% (once ever 300 trials)
• 4-sigma is 0.00669% (once every 15000 trials)
• 5-sigma is 5.9e-05% (once every 1,700,000 trials)
• 6-sigma is 2e-07% (once every 500,000,000)

for

Measuring sigma events

Take 300 measures after warmup, and measure the worst relative deviation

$ for i in {1..10}; do sudo ./sigma_test; done
4.56151
4.904
7.43446
5.73425
9.89544
12.975
3.92584
3.14633
4.91766
5.3699

What if we dealt with log-normal distributions?

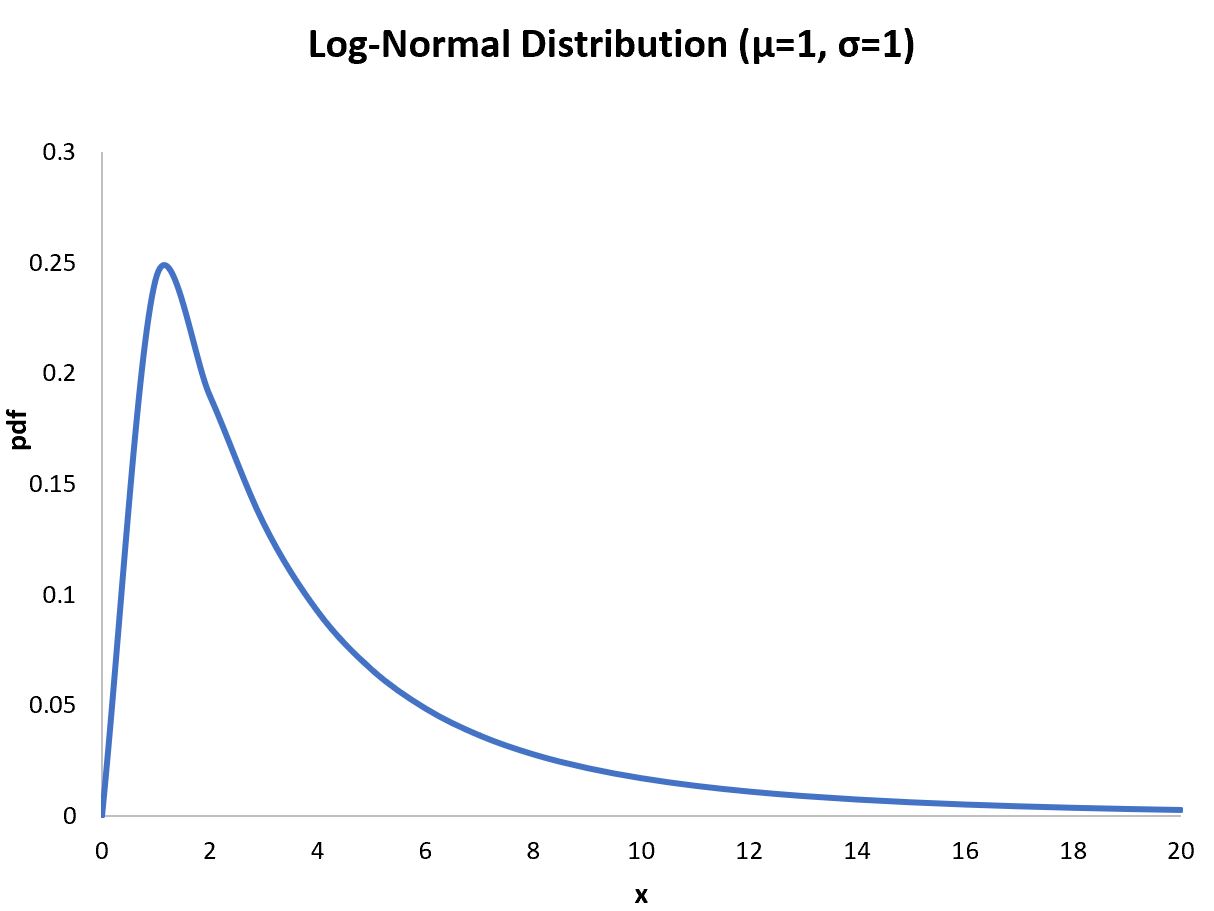
for N in range(20, 2000+1):
    s = [sum(np.random.default_rng().lognormal(1, 4, N))/N for i in range(30)]
    print(N,np.std(s))

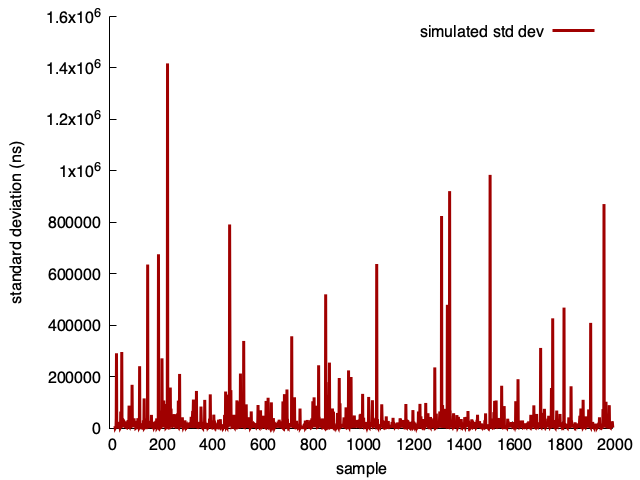
What if we measured the minimum?

Relative standard deviation ()

• The minimum is easier to measure to 1% accuracy.

CPU performance counters

Processors have zero-overhead counters recording instruction retired, actual cycles, and so forth.

No need to freeze the CPU frequency: you can measure it.

Limitations

• You can only measure so many things (2, 4 metrics, not 25)
• Required privileged access (e.g., root)

Counters in the cloud

• x64: Requires at least a full CPU
• ARM Graviton: generally available but limited number (e.g., 2 counters)

Instruction counts are accurate

Using performance counters

• Java instruction counters: https://github.com/jvm-profiling-tools/async-profiler
• C/C++: instruction counters are available through the Linux kernel
• Go instruction counters

Generally, fewer instructions means faster code

• Some instructions are more expensive than others (e.g., division).
• Data dependency can make instruction counts less relevant.
• Branching can artificially lower instruction count.

If you are adding speculative branching, make sure your test input is large.

while (howmany != 0) {
    val = random();
    if( val is an odd integer ) {
      out[index] =  val;
      index += 1;
    }
    howmany--;
}

2000 'random' elements, AMD Rome

Take away 1

• Computational microbenchmarks can have log-normal distributions.
• Consider measuring the minimum instead of the average.

Take away 2

• Benchmarking often is good
• Long-running benchmarks are not necessarily more accurate.
• Prefer cheap, well-designed benchmarks.

Links

• Blog https://lemire.me/blog/
• Twitter: @lemire
• GitHub: https://github.com/lemire