Floating-point number parsing with perfect accuracy at a gigabyte per second

Daniel Lemire
professor, Université du Québec (TÉLUQ)
Montreal

blog: https://lemire.me
X: @lemire
GitHub: https://github.com/lemire/

work with Michael Eisel, Ivan Smirnov, Nigel Tao, R. Oudompheng, Carl Verret and others!

How fast is your disk?

• PCIe 4 disks: 5 GB/s reading speed (sequential)
• PCIe 5 disks: 14.5 GB/s (0.20$/GB)

Fact

Single-core processes are often CPU bound

How fast can you ingest data?

{ "type": "FeatureCollection",
  "features": [
[[[-65.613616999999977,43.420273000000009],
[-65.619720000000029,43.418052999999986],
[-65.625,43.421379000000059],
[-65.636123999999882,43.449714999999969],
[-65.633056999999951,43.474709000000132],
[-65.611389000000031,43.513054000000068],
[-65.605835000000013,43.516105999999979],
[-65.598343,43.515830999999935],
[-65.566101000000003,43.508331000000055],
...

How fast can you parse numbers?

std::stringstream in(mystring);
while(in >> x) {
   sum += x;
}
return sum;

50 MB/s (Linux, GCC -O3)

Source: https://lemire.me/blog/2019/10/26/how-expensive-is-it-to-parse-numbers-from-a-string-in-c/

Some arithmetic

5 GB/s divided by 50 MB/s is 100.

Got 100 CPU cores?

Want to cause climate change all on your own?

How to go faster?

• Fewer instructions (simpler code)
• Fewer branches

How fast can you go?

AMD Rome (Zen 2). GNU GCC 10, -O3.

17-digit mantissa, random in [0,1].

Floats are easy

• Standard in Java, Go, Python, Swift, JavaScript...
• IEEE standard well supported on all recent systems
• 64-bit floats can represent all integers up to exactly.

Floats are hard

> 0.1 + 0.2 == 0.3
false

Generic rules regarding "exact" IEEE support

• Always round to nearest floating-point number (*,+,/)
• Resolve ties by rounding to nearest with an even decimal mantissa/significand.

Benefits

• Predictable outcomes.
• Debuggability.
• Cross-language compatibility (same results).

Challenges

• Machine A writes float to string
• Machine B reads string gets float
• Machine C reads string gets float

Do you have and ?

What is the problem?

Need to go from

(e.g., 123e5)

to

Example

0.10000000000000000555

0.2000000000000000111

0.29999999999999998889776975

Problems

Start with 32323232132321321111e124.

Lookup as a float (not exact)

Convert 32323232132321321111 to a float (not exact)

Compute

Approximation Approximation = Even worse approximation!

Insight

You can always represent floats exactly (binary64) using at most 17 digits.

Never to this:

3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679

credit: xkcd

We have 64-bit processors

So we can express all positive floats as
12345678901234567E+/-123.

Or

where mantissa

But fits in a 64-bit word!

Factorization

Overall algorithm

• Parse decimal mantissa to a 64-bit word!
• Precompute for all powers with up to 128-bit accuracy.
• Multiply!
• Figure out right power of two

Tricks:

• Deal with "subnormals"
• Handle excessively large numbers (infinity)
• Round-to-nearest, tie to even

SIMD

• Stands for Single instruction, multiple data
• Allows us to process 16 bytes or more with one instruction
• Supported on all modern CPUs (phone, laptop)
• Not portable

SWAR

• Stands for SIMD within a register
• Use normal instructions, portable (in C, C++,...)
• A 64-bit register can be viewed as 8 bytes
• Requires some cleverness

Check whether we have a digit

In ASCII/UTF-8, the digits 0, 1, ..., 9 have values
0x30, 0x31, ..., 0x39.

To recognize a digit:

• The high nibble should be 3.
• The high nibble should remain 3 if we add 6 (0x39 + 0x6 is 0x3f)

Silly formula to recognize a digit

Check whether we have 8 consecutive digits

bool is_made_of_eight_digits_fast(const char *chars) {
  uint64_t val;
  memcpy(&val, chars, 8);
  return (((val & 0xF0F0F0F0F0F0F0F0) |
           (((val + 0x0606060606060606) & 0xF0F0F0F0F0F0F0F0) >> 4)) 
           == 0x3333333333333333);
}

(Works with ASCII, harder if input is UTF-16 as in Java/C#)

Then construct the corresponding integer

Using only three multiplications (instead of 7):

 uint32_t parse_eight_digits_unrolled(const char *chars) {
  uint64_t val;
  memcpy(&val, chars, sizeof(uint64_t));
  val = (val & 0x0F0F0F0F0F0F0F0F) * 2561 >> 8;
  val = (val & 0x00FF00FF00FF00FF) * 6553601 >> 16;
  return (val & 0x0000FFFF0000FFFF) * 42949672960001 >> 32;
}

Positive powers

• Compute where is only approximate (128 bits)
• Maybe surprisingly, 128-bit precision is all that is needed to always get exact results.

Noble Mushtak, Daniel Lemire, Fast Number Parsing Without Fallback Software: Practice and Experience 53 (7), 2023

Negative powers

• Compilers replace division by constants with multiply and shift

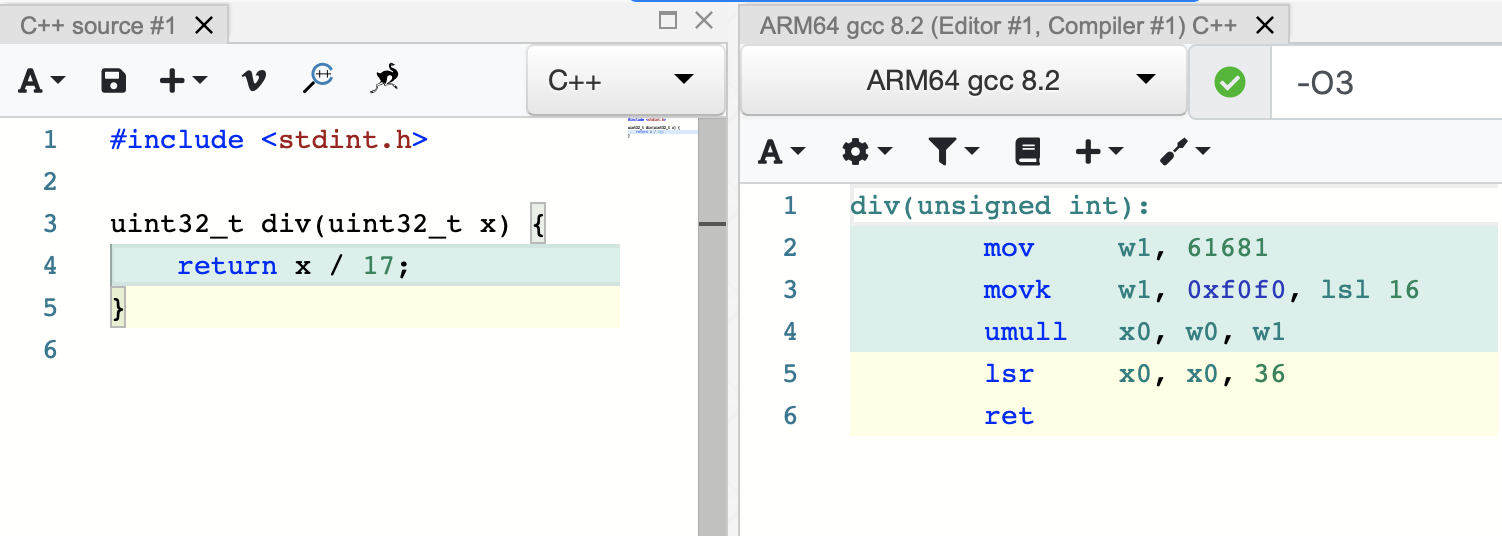
credit: godbolt

Reading: Integer Division by Constants: Optimal Bounds, https://arxiv.org/abs/2012.12369

Negative powers

• Precompute (reciprocal, 128-bit precision)
• Always get exact results.

What about tie to even?

• Need absolutely exact mantissa computation, to infinite precision.

• But only happens for small decimal powers () where absolutely exact results are practical.

What if you have more than 19 digits?

• Truncate the mantissa to 19 digits, map to .
• Do the work for
• Do the work for
• When get same results, you are done. (99% of the time)

Overall

• With 64-bit mantissa.
• With 128-bit powers of five.
• Can do exact computation 99.99% of the time.
• Fast, cheap, accurate.

Full product?

• 64-bit 64-bit 128-bit product
• GNU GCC: __uint128_t.
• Microsoft Visual Studio: _umul128
• ARM intrinsic: __umulh
• Go: bits.Mul64
• C#: Math.BigMul

Leading zeros

• How many consecutive leading zeros in 64-bit word?
• GNU GCC: __builtin_clzll
• Microsoft Visual Studio: _BitScanReverse64
• C++20: std::countl_zero
• Go: bits.LeadingZeros64
• C#: BitOperations.LeadingZeroCount

C/C++

• https://github.com/lemire/fast_float

• GNU GCC

• LLVM clang

• used by Apache Arrow, Yandex ClickHouse, Microsoft LightGBM

Go

• Algorithm adapted to Go's standard library (ParseFloat) by Nigel Tao and others

• Release notes (version 1.16): ParseFloat (...) improving performance by up to a factor of 2.

• Perfect rounding.

• Blog post by Tao: The Eisel-Lemire ParseNumberF64 Algorithm

Rust

R

rcppfastfloat: https://github.com/eddelbuettel/rcppfastfloat

3x faster than standard library

C#

FastFloat.ParseDouble is 5x faster than standard library (Double.Parse)

https://github.com/CarlVerret/csFastFloat/

credit: Carl Verret, Egor Bogatov (Microsoft) and others

Further reading

• Noble Mushtak, Daniel Lemire, Fast Number Parsing Without Fallback, Software: Practice and Experience 53 (7), 2023
• Daniel Lemire, Number Parsing at a Gigabyte per Second,
  Software: Practice and Experience 51 (8), 2021
• Blog: https://lemire.me/blog/